一些基本概念与前置知识
量子比特
叠加态
和经典比特只有0和1两种确定的状态不同,量子比特具有两种可能的状态——\(|0\rangle\)和\(|1\rangle\),但只有当它被观测时,才能确定到底是哪种状态,其余时刻处于叠加态,也就是上面两种状态的线性组合: $$ |\psi\rangle = \alpha|0\rangle + \beta|1\rangle $$ 其中\(\alpha\)和\(\beta\)都是复数(将其视为实数一般也不会有问题)
测量
当我们去测量某个比特时,会坍缩到一个确定的状态上——\(|\alpha|^2\)的概率为0,\(|\beta|^2\)的概率为1 $$ \begin{aligned} P(0) &= |\alpha|^2\\ P(1) &= |\beta|^2 \end{aligned} $$ 显然,\(|\alpha|^2 + |\beta|^2 = 1\)。所以,量子比特可以用二维复向量空间中的单位向量表示
我们定义一个特殊的状态\(|+\rangle\): $$ |+\rangle = \frac{1}{\sqrt 2} |0\rangle + \frac{1}{\sqrt 2} |1\rangle $$ 显然,对于它而言,观测时0和1出现的概率都是50%
几何表示
通过欧拉公式,可以将上面的表达式转化为这样的形式(因为第一行括号外的系数不影响观测到的状态,所以可以省去): $$ \begin{aligned} |\psi\rangle &= e^{\mathrm i\gamma} \left(\cos \frac \theta 2 |0\rangle + e^{\mathrm i \varphi}\sin \frac\theta 2|1\rangle \right)\\ &\Rightarrow\cos \frac\theta 2 |0\rangle + e^{\mathrm i \varphi}\sin \frac\theta 2 |1\rangle \end{aligned} $$ \(\theta\)和\(\varphi\)分别对应了布洛赫球面上与\(x\)轴和\(z\)轴的夹角
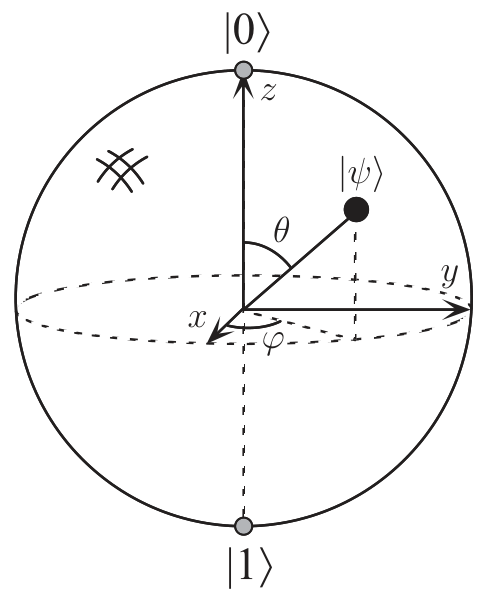
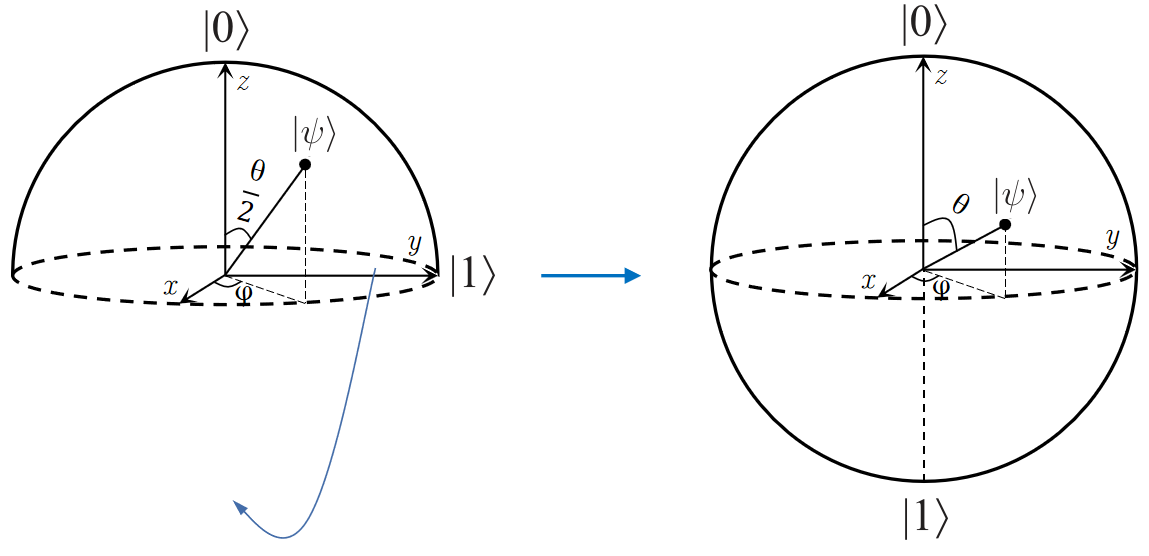
注意到,公式中的是\(\theta/2\)而非\(\theta\),是因为正余弦函数中的角度取值范围实是\([0, \pi/2]\),是一个半球壳。但为了方便处理,我们将其「拉升」为一个完整的球体
多量子比特
- 双量子比特
更新中……